|
|
发表于 2017-2-18 13:22
|
显示全部楼层
来自： 中国上海
A permanent magnet synchronous generator is a generator where the excitation field is provided by a permanent magnet instead of a coil. The term synchronous refers here to the fact that the rotor and magnetic field rotate with the same speed, because the magnetic field is generated through a shaft mounted permanent magnet mechanism and current is induced into the stationary armature
Synchronous generators are the majority source of commercial electrical energy. They are commonly used to convert the mechanical power output of steam turbines, gas turbines, reciprocating engines and hydro turbines into electrical power for the grid. Some designs of Wind turbines also use this generator type.
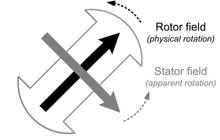
In the majority of designs the rotating assembly in the center of the generator—the "rotor"—contains the magnet, and the "stator" is the stationary armature that is electrically connected to a load. As shown in the diagram above, the perpendicular component of the stator field affects the torque while the parallel component affects the voltage. The load supplied by the generator determines the voltage. If the load is inductive, then the angle between the rotar and stator fields will be greater than 90 degrees which corresponds to an increased generator voltage. This is known as an overexcited generator. The opposite is true for a generator supplying a capacitive load which is known as an underexcited generator. A set of three conductors make up the armature winding in standard utility equipment, constituting three phases of a power circuit—that correspond to the three wires we are accustomed to see on transmission lines. The phases are wound such that they are 120 degrees apart spatially on the stator, providing for a uniform force or torque on the generator rotor. The uniformity of the torque arises because the magnetic fields resulting from the induced currents in the three conductors of the armature winding combine spatially in such a way as to resemble the magnetic field of a single, rotating magnet. This stator magnetic field or "stator field" appears as a steady rotating field and spins at the same frequency as the rotor when the rotor contains a single dipole magnetic field. The two fields move in "synchronicity" and maintain a fixed position relative to each other as they spin.[1]
They are known as synchronous generators because f, the frequency of the induced voltage in the stator (armature conductors) conventionally measured in hertz, is directly proportional to RPM, the rotation rate of the rotor usually given in revolutions per minute (or angular speed). If the rotor windings are arranged in such a way as to produce the effect of more than two magnetic poles, then each physical revolution of the rotor results in more magnetic poles moving past the armature windings. Each passing of a north and south pole corresponds to a complete "cycle" of a magnet field oscillation. Therefore, the constant of proportionality is P 120 {\displaystyle {\frac {\text{P}}{120}}}  , where P is the number of magnetic rotor poles (almost always an even number), and the factor of 120 comes from 60 seconds per minute and two poles in a single magnet; f ( Hz ) = R P M P 120 {\displaystyle f\left({\text{Hz}}\right)=RPM{\frac {\text{P}}{120}}}  .[2]
The power in the prime mover is a function of RPM and torque. P m = T m ∗ R P M {\displaystyle P_{m}=T_{m}*RPM}  where P m {\displaystyle P_{m}}  is mechanical power in Watts, T m {\displaystyle T_{m}}  is the torque with units of N ∗ m r a d {\displaystyle {\frac {N*m}{rad}}}  , and RPM is the rotations per minute which is multiplied by a factor of 2 π {\displaystyle 2\pi }  to give units of R a d i a n s S e c {\displaystyle {\frac {Radians}{Sec}}}  . By increasing the torque on the prime mover, a larger electrical power output can be generated.
In practice, the typical load is inductive in nature. The diagram above depicts such an arrangement. E i {\displaystyle E_{i}}  is the voltage of the generator, and V a {\displaystyle V_{a}}  and I a {\displaystyle I_{a}}  are the voltage and the current in the load respectively and θ {\displaystyle \theta }  is the angle between them. Here, we can see that the resistance, R, and the reactance, X d {\displaystyle X_{d}}  , play a role in determining the angle δ {\displaystyle \delta }  . This information can be used to determine the real and reactive power output from the generator.
In this diagram, V t {\displaystyle V_{t}}  is the terminal voltage. If we ignore the resistance as shown above, we find that the power can be calculated:[3]
I a = | E i | ∠ δ − | V t | j X d {\displaystyle I_{a}={\frac {|E_{i}|\angle \delta -|V_{t}|}{jX_{d}}}}
S = P + j Q = V t I ⋆ = | V t | | E i | ∠ ( − δ ) − | V t | 2 − j X d = | V t | | E i | ( c o s ( δ ) − j s i n ( δ ) ) − | V t | 2 − j X d {\displaystyle S=P+jQ=V_{t}I^{\star }={\frac {|V_{t}||E_{i}|\angle (-\delta )-|V_{t}|^{2}}{-jX_{d}}}={\frac {|V_{t}||E_{i}|(cos(\delta )-jsin(\delta ))-|V_{t}|^{2}}{-jX_{d}}}}
Breaking the apparent power into Real and Reactive power, we get:
P = | V t | | E i | X d s i n ( δ ) {\displaystyle P={\frac {|V_{t}||E_{i}|}{X_{d}}}sin(\delta )}
, Q = | V t | X d ( | E i | c o s ( δ ) − | V t | ) {\displaystyle Q={\frac {|V_{t}|}{X_{d}}}(|E_{i}|cos(\delta )-|V_{t}|)}
In a permanent magnet generator, the magnetic field of the rotor is produced by permanent magnets. Other types of generator use electromagnets to produce a magnetic field in a rotor winding. The direct current in the rotor field winding is fed through a slip-ring assembly or provided by a brushless exciter on the same shaft.
Permanent magnet generators (PMG's) or alternators (PMA's) do not require a DC supply for the excitation circuit, nor do they have slip rings and contact brushes. The future economics of PMA's or PMG's as they are sometimes called is now largely co***olled by China as they have the global monopoly on neodymium material used to make the most powerful and also the most desirable types of magnets used today. The flux density of high performance permanent magnets is limited giving China an unfair advantage in setting the global price. A key disadvantage in PMA's or PMG's is that the air gap flux is not co***ollable, so the voltage of the machine cannot be easily regulated. A persistent magnetic field imposes safety issues during assembly, field service or repair. High performance permanent magnets, themselves, have structural and thermal issues. Torque current MMF vectorially combines with the persistent flux of permanent magnets, which leads to higher air-gap flux density and eventually, core saturation. In this permanent magnet alternators the speed is directly proportional to the output voltage of the alternator.
|
|
楼主: DraftMan
